Extended Summary
[abstract]
1. Introduction
Amplitude fluctuation is a manifestation of wave interference and consists of
variations in the maximum value of sound signals (i.e. amplitude) as measured relative to a reference point. The rate, degree, and shape of a complex signal's amplitude fluctuations are variables that are manipulated
by musicians around the world to exploit the sensations of beating and roughness, making amplitude fluctuation a
significant expressive tool in the production of musical sound.
The history of the understanding of the physical
and perceptual properties of waves in general and of amplitude fluctuations in particular is reviewed, drawing from
the areas of music, ethnomusicology, acoustics, psychoacoustics, and
engineering. In spite of overwhelming evidence
on the energy content of amplitude fluctuation, the related literature contains conflicting opinions regarding its
physical properties, as well as inconsistencies in its graphical representation and manipulation. As a result, there are similar inconsistencies with regards to the possible perceptual attributes of amplitude fluctuation,
hindering the understanding of its musical significance. The erroneous assumption that signal amplitude fluctuations
represent temporal patterns that carry no energy appears to persist mainly because of reports from dichotic experiments. Consequently, the issue of the physical and perceptual properties of amplitude fluctuation has remained unresolved,
justifying the need for the present study. This abstract outlines the study findings and discusses possibilities for future research.
2. Degree of Amplitude Fluctuation versus Amplitude Modulation Depth
Contrary to convention, degree of amplitude fluctuation (AF-degree) and amplitude modulation depth (AM-depth) are different
both conceptually and quantitatively. AF-degree refers to a signal's degree of amplitude fluctuation, while AM-depth
refers to a signal's degree of spectral energy spread. Whenever AM-depth values are used as a measure of a modulated signal's
AF-degree, modulation implementation produces an error arising from the nonlinear relationship between the presumed and
applied AF-degrees.
It is shown that, in order to apply an intended AF-degree, an adjusted coefficient must be inserted in
the modulation implementation equation. This adjustment influences the interpretation of studies where presumed changes
in AF-degree have been correlated to changes in physical, physiological, or psychological
measurements. In a study by Terhardt (1974), for example, the identified error provided unjustified support to a hypothesis of a neural low-pass
weighting mechanism operating on a signal's temporal envelope. Additionally, it has supported roughness estimation
models of complex spectra that largely underestimate the influence of the degree of amplitude fluctuation to the
roughness of complex tones.
As a general observation, the erroneous assumption of the equivalence between amplitude
modulation and amplitude fluctuation has resulted in the misinterpretation of studies examining perceptual correlates of
amplitude fluctuation, providing questionable support to related perceptual
models. Psychometric functions from studies that
have miscalculated the degree of amplitude fluctuation have been distorted by a factor proportional to the
error. The influence
of the proposed adjustment to the interpretation of distorted psychometric functions will vary according to the meaning
attributed by each study to each specific function's shape. Careful reexamination of such studies is necessary, especially
if their results constitute the principal support to a larger model.
The present dissertation kept the terms amplitude
modulation and amplitude fluctuation separate and adopted the term amplitude fluctuation to refer specifically to variations
in a signal's amplitude around a reference value.
3. Theoretical and Experimental Examination of the Wave Energy Carried by Amplitude Fluctuations
Sound wave interference gives rise to amplitude fluctuations, indicating that the perception of sound interference products
may be a manifestation of amplitude fluctuation energy. It is argued that modulations in general and amplitude fluctuations
in particular satisfy all criteria that define a wave. The energy content of amplitude fluctuations is investigated in
an effort to provide theoretical and experimental support to the large amount of evidence demonstrating energy transfer
at the rate of amplitude fluctuation. Although air is a non-dispersive medium, the dispersive case is also addressed because
it facilitates the analysis of the kinematic properties of modulated
waves. Introducing the concept of dispersion to the study
of musical sound is not unusual. Sound diffraction, absorption, and reverberation have all been better understood with the
aid of dispersion theory.
A theoretical value for the amplitude fluctuation energy is calculated for the simplified case of a single point-source oscillating at two angular frequencies
w1, w2- with the same amplitudes
A1 = A2 = A, and zero initial phases.
Assuming that the conditions permitting linear addition of wave energy quantities are satisfied,
the application of the energy conservation law to the equation describing a two-component complex
wave as a sine wave with fluctuating amplitude indicates a power difference between the two sides of the equation. This difference is interpreted as the power radiated by the fluctuations and is equivalent to the
power radiated by a point-source pulsating with angular frequency
wAF =|w1-w2|
(amplitude fluctuation rate) and amplitude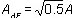 
= 0.707A.
The theoretical values for the frequency and amplitude of the fluctuation component are compared to values obtained through
Hilbert demodulation and Frequency-Zoom analysis. The analysis reveals a single component with frequency equal to the experiment
signal's amplitude fluctuation rate, providing clear evidence of the energy content of amplitude fluctuations.
However, the amplitude value of the fluctuation component indicated by the analysis (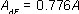 ) is different from the predicted value. The discrepancy between predicted and observed amplitudes may be attributed to possible violations of the assumptions underlying
the application of the energy conservation law, as well as to inadequate protection from analysis errors due to spectral leakage. The results confirm the energy content of amplitude fluctuation but are quantitatively inconclusive, warranting further study.
The theoretical model proposed is limited to the simplest possible case and relies on energy conservation assumptions that further
restrict its use. A more suitable model would be based on a valid modification / simplification of the generalized expressions
for the pressure at the difference frequency (in Hamilton, 1998: 223-225). Additionally, the methods employed to empirically verify
the predictions of the proposed model are indirect and prone to analysis errors. A direct experimental method would employ
non-intrusive measurement techniques (e.g. laser vibrometry), applied on finely tuned resonators exposed to the experiment signal
and placed within an environment isolated from external vibrations.
4. Alternative Representation of Sound Waves for Better Illustration of Wave Energy Quantities
An alternative sound signal representation is proposed that represents graphically the energy content of amplitude fluctuations
and solves numerous problems associated with traditional two-dimensional
signals. The new signal representation is based on
the complex equation of motion and includes both the sine (imaginary) and cosine (real) terms describing a vibration.
It results in spiral sine signals and twisted-spiral complex signals, similar to complex analytic signals. Three-dimensional signals illustrate that amplitude fluctuations and the signal envelopes that describe them are not just
boundary curves. Rather, they are waves that trace changes in the total instantaneous energy of a signal over time, representing
the oscillation between potential and kinetic energies within a wave.
Three-dimensional sound signals are not intended to
replace their two-dimensional counterparts but to inform them. Spiral sine signals offer a consistent measure of the energy
content of sine waves across frequencies, while twisted spiral complex signals account for the negative amplitude values predicted
by the mathematical expression of amplitude fluctuation, map the parameters of amplitude fluctuation onto the twisting parameters,
and paint a more realistic picture of wave propagation. Developing software that displays in real time an arbitrary, user-defined
complex wave in three dimensions, as a twisted spiral, will contribute to the better understanding of sound wave propagation in air.
5. Sound Interference Products and Wave Interaction at a Neural Level
The fact that amplitude fluctuations carry energy has been challenged by previous experiments where sound interference products
appear to arise at a neural level. The possibility of interference products arising from neural wave interaction is examined
through a series of dichotic experiments. It is shown that the perception of sound interference in terms of loudness changes,
beating, or roughness does not arise unless sound waves interact
physically. Three sets of dichotic experiments confirm this claim.
The first experiment examines the possibility of beating when a sine stimulus is presented to both ears through headphones. In this case, diplacusis causes a pitch difference between the two ears that would introduce beating if neural wave interaction
could give rise to interference products. However, no such beating is
observed.
The second set of experiments examines the effect
of phase on dichotically presented sine stimuli. Results indicate that changes in the phase relationship between the left and
right channels of dichotic sine signals give rise to perceptions that are incompatible with the interference principle and
consistent with results from studies that have established phase differences between ears as sound localization cues. It is shown that:
1. Changing the phase relationship between the left and right channels of a sinusoidal stimulus presented
dichotically does not change its loudness.
2. For frequencies <500Hz (i.e. 200Hz & 300Hz), dichotic phase changes affect the perceived direction of a stimulus, with
1800 phase difference resulting in a wider stereo image.
3. For frequencies >1500Hz (i.e. 1700Hz & 2500Hz), dichotic phase changes introduce no perceptual change.
The third experiment is based on the above results and tests whether the beating-like sensation reported in previous dichotic
experiments is an indication of interference products arising at a neural level or rather the manifestation of a sound localization
mechanism based on phase difference cues. It is shown that, in dichotic explorations of beats, the constantly shifting phase between
the sine components presented in the two ears results in a constantly shifting localization of the two-component complex stimulus.
For low frequency differences this shift is interpreted as a rotation of the sound inside the subject's head and, for higher
frequency differences it is interpreted as a timbral fluctuation that is often confused by the subjects with loudness
fluctuation / beating. Consistent with sound localization studies and contrary to the interference principle, two-component
dichotic stimuli with different frequencies in each ear are treated perceptually as rotating sines for frequencies <500Hz.
For frequencies >1500Hz they are treated as steady sines, with the frequency difference between ears introducing no perceptual
difference.
The findings support the hypothesis against sound interference products arising due to neural wave interaction. They are consistent with the arguments for the energy content of amplitude fluctuation and indicate that the beating sensation
reported in previous dichotic experiments must have been a misidentified rotating sensation.
6. Auditory Roughness Estimation of Complex Spectra - Roughness Degrees and Harmonic Interval Dissonance Ratings within
the
Western Musical Tradition
Examination of musical instrument construction and performance practice illustrates the musical relevance of amplitude
fluctuation energy and indicates that sound variations involving the sensation of roughness are found in most musical traditions. A new roughness estimation model is proposed that better represents the theoretical knowledge and experimental results on
sensory roughness and is better fit to test hypotheses linking the roughness sensation to musical variables.
It is argued that existing models estimating the roughness of pairs of sines demonstrate limited predictive power because they:
1. underestimate the contribution of AF-degree (i.e. relative amplitudes values of the interfering sines) to roughness,
2. overestimate the contribution of sound pressure level (i.e. absolute amplitude values of the interfering sines) to roughness, and
3. misrepresent the relationship between roughness and register.
Based on the roughness estimation model introduced by Sethares (1998), a new model is proposed, which includes a term to
account for the contribution of the amplitudes of interfering sines to the roughness of a
sine-pair. This term is based
on existing experimental results (von Békésy, 1960; Terhardt, 1974), adjusted to account for the quantitative difference
between AM-depth and AF-degree identified by the present study. The roughness of complex spectra with more than two sine
components is estimated by adding together the roughness of the individual
sine-pairs. The proposed model does not account
for the influence of phase on roughness and is not fit to handle continuous
spectra. To ensure the reliability of the model,
the complex spectra examined must: a) have components with the same initial phase or less than three components per critical band,
b) correspond to signals that are relatively symmetrical along the time axis, and c) be
discrete. Under these conditions, the
proposed model constitutes a good representation of the theoretical knowledge and empirical data on the roughness of complex spectra.
The model is tested experimentally against two earlier roughness estimation models (Helmholtz, 1885; Hutchinson & Knopoff, 1978),
and all three models are applied to a hypothesis linking the consonance hierarchy of harmonic intervals, within the Western
chromatic scale, to roughness variations. The predictions of the three models differ in several respects. The majority of differences can be explained in terms of the assumptions each model makes regarding the contributions of
AF-degree and of sound pressure level to roughness. The proposed model demonstrates the best agreement between estimated and observed
roughness as well as between estimated roughness and observed dissonance.
The empirical results indicate that the clear
presence or absence of roughness in the sound of an interval dominates dissonance
ratings. When the roughness is neither very
large nor very small, decisions on dissonance often ignore roughness and are culturally and historically
mediated. Overall, dissonance
ratings correlate well with roughness ratings, indicating that, in the case of isolated harmonic intervals, the sensation of
roughness is the primary cue guiding dissonance judgments. The results support the hypothesis that, in the Western musical
tradition where sensory roughness is in general avoided as dissonant, the consonance hierarchy of harmonic intervals corresponds
to variations in roughness degrees.
The validity and utility of the proposed roughness estimation model can be improved significantly through a series of
theoretical and practical modifications. The following steps would remove the limiting conditions imposed on the model
with regards to the effects of phase and of signal envelope asymmetry on roughness:
1. Two functions must be introduced. One to describe the relationship between the relative phase of three interfering sines
and the degree of amplitude fluctuation of the three-component signal, and a second one to quantify signal envelope asymmetry.
2. Two sets of perceptual experiment must be conducted. One to examine the roughness relationship between AM tones with a
specified AF-degree and AM tones with the same AF-degree arrived at through phase manipulation, and a second one to
examine the effect of signal envelope asymmetry on roughness.
3. Two coefficients must be added to the proposed roughness estimation model, implementing the results from the previous steps.
The modified model will represent a comprehensive account of the current knowledge on sensory roughness and will be valid
to the examination of all discrete spectra.
To improve the utility of the proposed model and make it available to a great variety of research questions a computer
application may be created that will:
1. perform spectral analysis on incoming sound signals at user-specified time intervals and measure the signal's
degree of asymmetry based on the previously identified asymmetry function;
2. process the spectral analysis results based on an algorithm that selects the significant (according to user-specified criteria)
components of the spectrum and output a frequency, an amplitude, and a phase value for each selected component;
3. supply the frequency, amplitude, phase, and asymmetry values to the roughness estimation model;
4. provide numerical and graphical versions of the model's output.
An application such as the one described would enable the empirical testing of hypotheses linking roughness to concepts of
musical tension, release, stability, etc., which are temporal and cannot be addressed efficiently by calculating the roughness
of isolated sonorities. Additionally, automating the roughness estimation process would make the model easy to apply,
guaranteeing its use in future research.
7. Manipulation of Amplitude Fluctuation and Musical Expression
Amplitude fluctuation constitutes the most common time-variant characteristic of musical
sounds. The large variety of perceptual
possibilities introduced through the manipulation of amplitude fluctuation (e.g. beating, roughness, combination tones) has been
exploited by numerous musical traditions throughout history. Manipulating the degree and rate of amplitude fluctuation helps
create a shimmering (e.g. Indonesian gamelan performances), buzzing (e.g. Indian tambura drone), or rattling (e.g. Bosnian ganga singing) sonic canvas that becomes the backdrop for further musical
elaboration. It permits the creation of timbral
(e.g. Middle Eastern mijwiz playing) or even rhythmic (e.g. ganga singing) variations through gradual or abrupt changes
between fluctuation rates and degrees. Whether such variations are explicitly sought for (as in ganga singing and mijwiz playing)
or are introduced more subtly and gradually (as may be the case in the typical chord progressions / modulations of Western music),
they have both sonic and symbolic significance and form an important part of a musical tradition's expressive
vocabulary. Important
clues regarding the ways various musical cultures approach the perceptual attributes of amplitude fluctuation are identified through
an examination of musical instrument construction and performance
practice. The examples sited in the dissertation help illustrate
the significance of a study on amplitude fluctuation to music.
Explicit understanding of the physical variables associated with the various aspects of musical sound is not a prerequisite to
music making or music appreciation. Music has been produced, listened to, and appreciated long before a good understanding
of the physical properties of sound had been reached. Such an understanding, however, is valuable in helping explain and
understand diverse musical choices and performance practices, as well as in offering the opportunity to explore new sonic
effects through the informed manipulation of physical variables. A Western musician may justify the use of certain harmonies
based on the concepts of consonance / dissonance, while a Bosnian singer may claim that narrow intervals are used partly because
they sound louder than unisons or wide intervals. Better understanding of the perceptual and physical properties of amplitude
fluctuation may lead to a better understanding of the basis of such
claims. Additionally, whenever a Bosnian listener judges a
Western piece of music as 'blunt' or a Western listener calls a ganga song 'offensive', perceptual differentiation has preceded
evaluative judgment.
Regardless of whether more or less beating / roughness is called for within a musical context, or whether a specific relationship
between interfering tones and difference tones is more desirable than others, being able to control their production allows
for the creation of finer sonic nuances. More importantly, it helps in appreciating that musical evaluations are based on cultural
ideals and do not map on levels of intellectual sophistication. All sounds, regardless of whether they are evaluated as 'good'
or 'bad', result from the manipulation of the same variables. The production of a musical sound that is considered 'bad',
within a musical tradition, may reflect a more sophisticated manipulation of certain sonic variables than the production of a
sound that is considered 'good'. The present study improves significantly the understanding of amplitude fluctuation by
examining musical practices considered, until recently, inferior. It is hoped that this work will motivate the growth of
cross-cultural, interdisciplinary research in musical sound and offer helpful tools for the analysis, understanding,
appreciation, and production of music.
REFERENCES
von Békésy, G. (1960). Experiments in Hearing. New York: Acoustical Society of America Press (1989).
Hamilton, M. F. (1998). Nonlinear effects in sound beams. In Handbook of
Acoustics,
M. J. Crocker, editor: 221-228.
New York: John Wiley & Sons, Inc.
Helmholtz, H. L. F. (1885). On the Sensations of Tone as a Physiological Basis for the
Theory of Music (2nd edition).
Trans. A. J. Ellis. New York: Dover Publications, Inc. (1954).
Hutchinson, W. and Knopoff, L. (1978). The acoustic component of Western
consonance. Interface, 7: 1-29.
Sethares, W. A. (1998). Tuning, Timbre, Spectrum, Scale. London: Springer-Verlag.
Terhardt, E. (1974). On the perception of periodic sound fluctuations (roughness).
Acustica, 30(4): 201-213.
|
